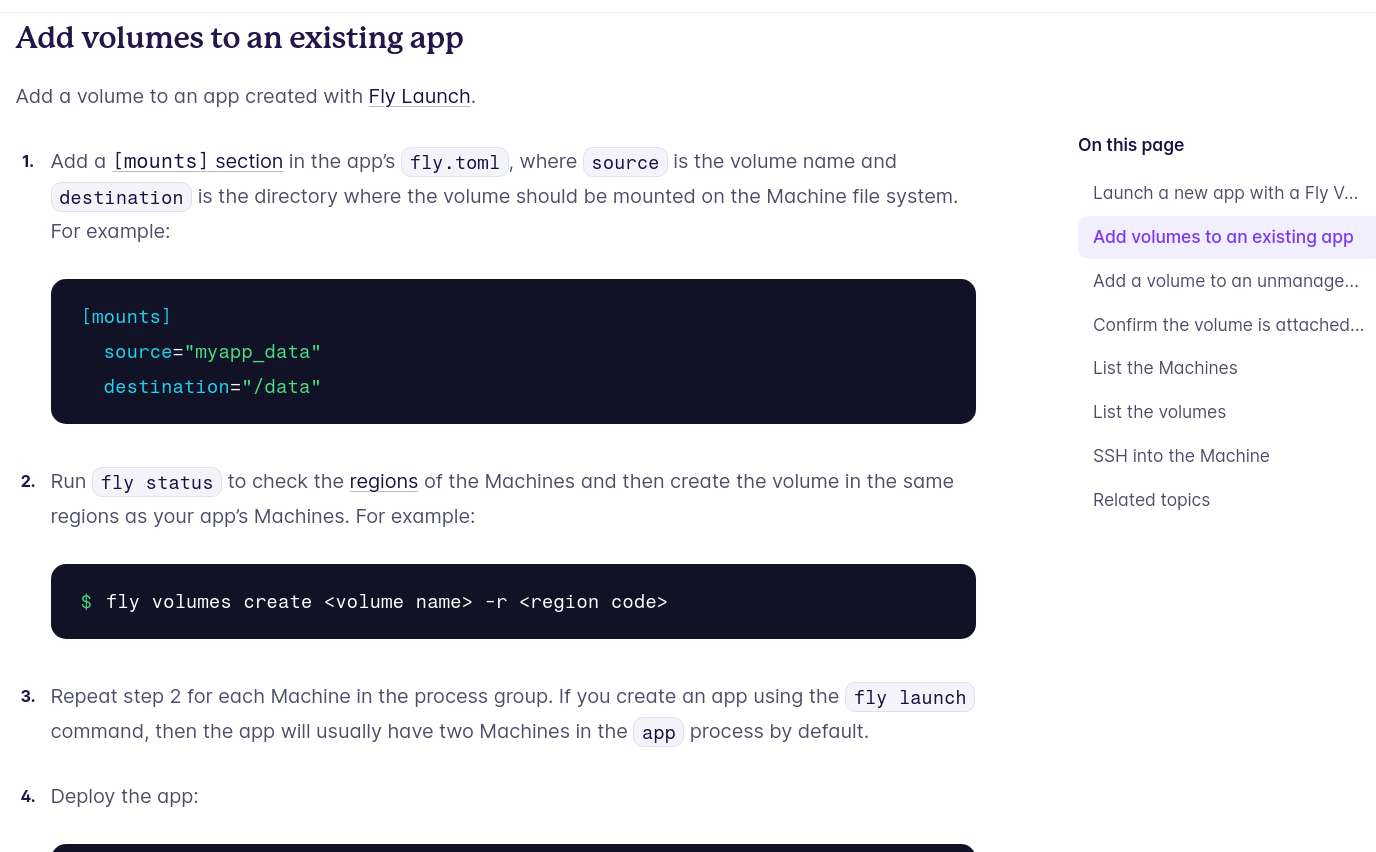
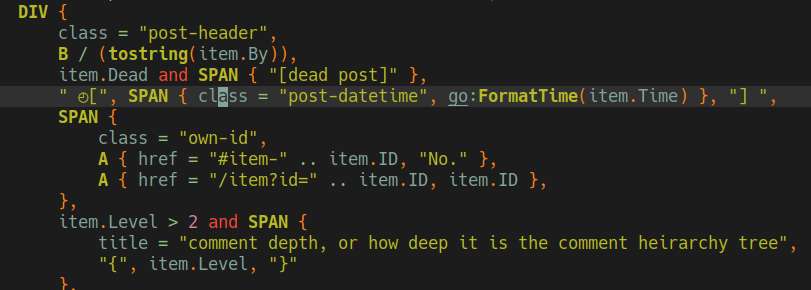
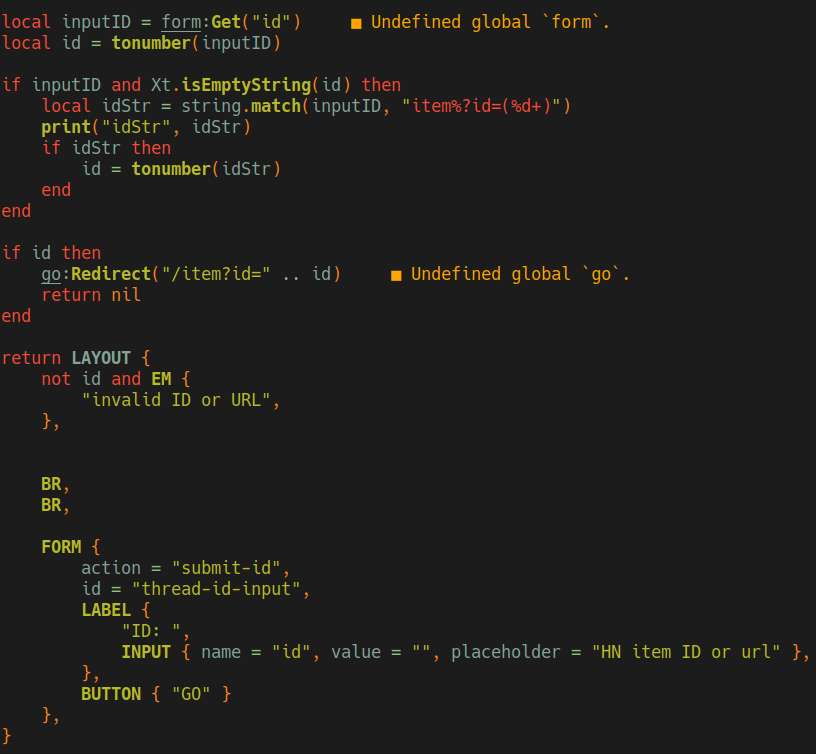
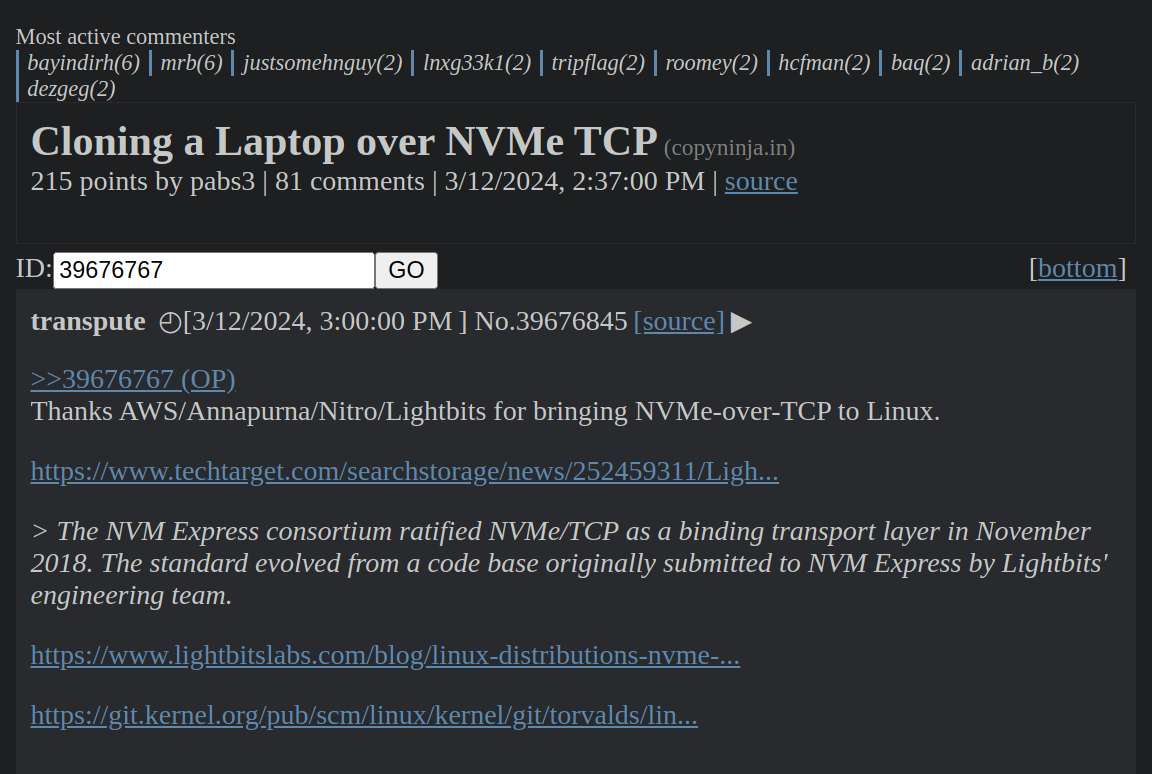
Worked on SN, I fixed the datetime so that it server-renders the date with UTC format, then converts that to localtime on the client side. I also added some textbox to easily view HN URLs.
I also looked at the fly logs why my cached json arent' working, it seems that they get deleted before the scheduled time. The logs says it periodically shutdowns the machine when the server is inactive. The fix is to use actual fly.io volumes for persistent storage.
And my quest to devise my own manual long division continues. I tried dividing and factoring several numbers numbers in my notebook, some small and some large-ish. Several observations:
- if I can't get rid of the ~, then it's (likely) not evenly divisible
- I can express larger numbers as a sum of exponential 10s such as: 123 = 1*10^2 + 2*10^1 + 3*10^0
- I should avoid distributing ~ over the sum, since it becomes even harder to solve
- Sometimes I have to add terms together to make them factorable
-
I can further factor these base exponentials to help see some factors:
So here, I could see at a glance that 735 is evenly divisible by 5, without doing full division or factoring.735 = 7*10^2 + 3*10^1 + 5 = 7*5*2*5*2 + 3*5*2 + 5 = 5(7*2*5*2 + 3*2 + 1) - Going further, I could try converting base10 to another baseN to help see the factors at a glance (in theory, I haven't tried)
With that, my division method would then be first to factor out the divisor and the dividend (prime factorization it's called it seems), then cancel out any inverses. To some extent, it works. I managed to do division even for larger numbers like 12345.
Sadly, this doesn't necessarily mean that if I don't see any obvious factors then it's a prime number. Naively I thought that was the case, I quickly ran into counterexamples, most damning of which is the quadruply nice number 469, which is a product of two prime numbers 7 and 67!?! My supposed method broke down, all is lost, god is dead and/or mad, what am I even doing with my life again.
Just kidding (maybe). I'm just missing some important detail.
469
= (2^4)(5^2) + (2^2)(3)(5) + 3(3)
469
= 6(7)Then a thought occured to me: what are real numbers? Do they even exist? Aren't they just an artifact of decimal notation? Of course, some math teacher would bonk me in the head, and point to irrational numbers. But no, what if I want to reject the concept of real numbers, out of uncalled spite, and that irrational numbers can be perfectly expressed as a ratio of two numbers, with some slight tweak in the notation and the base axioms. Maybe these dumb irrationals belong on a separate number line.
Okay, if I'm asking these crazy questions, it's time to take a break. I'll probably answer and disprove my own questions sooner or later as I go along.
To continue from yesterday, to find a way to do factoring and division, I have to ask, what does division mean anyway? What does evenly divisible mean? What's remainder? With some faint recollection of some wikipedia article, after some scribbling, I manage to come up with:
x = ab + cMoving stuffs around:
x = ab + c (1)
x - ab = c (2)
xa~ = b + ca~ (3)
xa~ = b
65 = 2*x + c
Let x = 31
65 = 2*31 + c
65 = 62 + c
65 - 62 = c
c = 3What about if I let Let x = 32
65 = 2*32 + c
65 = 64 + c
c = 1What does this all mean for me? What does a negative remainder mean, and why don't I see it in the wild? Setting that aside for now, from here it's clear that 65 cannot be evenly be divided by 2 (where c = 0). But if I want to divide by 2 anyway, I get 32 with a remainder of 1.
Checking it in python:
>>> 65/2
32.5
xa~ = b + ca~ (3)
65*2~ = 32 + 1*2~
= 32 + 0.5
= 32.5
32.5 = 32 + 5*10~
= 32 + 1*2~Then again, I still don't have a methodical approach of doing long division besides doing trial and error. On the other hand, I could now do fizzbuzz without using the modulo operator. Well, actually I already did that before using a weird alien assembly language , but still.